1. Suggested solutions weekly assignments - lectures 8 and 9

Experiment with the Galerkin and collocation methods and approximate the global functions

1. \(u(x) = |x|, \quad x \in [-1, 1]\)

2. \(u(x) = \exp(\sin(x)), \quad x \in [0, 2]\)

3. \(u(x) = x^{10}, \quad x \in [0, 1]\)

4. \(u(x) = \exp(-(x-0.5)^2) - \exp(-0.25) \quad x \in [0, 1]\)

5. \(u(x) = J_0(x), \quad x \in [0, 100]\)

where \(J_0(x)\) is the Bessel function of the first kind. The Bessel function is available both in Scipy and Sympy.

Below I will use the Galerkin method with Legendre or Chebyshev polynomials and the collocation method using Chebyshev points. Note that the code is a bit slow because the collocation method is not implemented very efficiently.

1.1. Use either Legendre or Chebyshev polynomials

First create some functions that can compute the (weighted) inner product \((u, v)_{\omega}\) for any domain \([a, b]\) by mapping to the reference domain \([-1, 1]\). Since the Legendre and Chebyshev polynomials use different weighting, the code will be a little bit different for the two.

import numpy as np
import sympy as sp 
from numpy.polynomial import Legendre, Chebyshev
import matplotlib.pyplot as plt
from scipy.integrate import quad
from lagrange import Lagrangebasis, Lagrangefunction
from scipy.interpolate import BarycentricInterpolator
x = sp.Symbol('x')

cj = lambda j: 2 if j == 0 else 1
Tj = lambda j, x: sp.cos(j * sp.acos(x))

def sq_L2_norm(j, space=Legendre):
    r"""Compute the square of the L2 norm for given basisfunction

    Parameters
    ----------
    j : int
        The basis number
    space : Class instance, optional
        Either Chebyshev or Lagrange 
    
    Return
    
    .. math::
    
        \|\psi_i\|^2_{\omega}
    
    """
    if space == Legendre:
        return sp.Rational(2, 2*j+1)
    elif space == Chebyshev:
        return cj(j)*sp.pi*sp.S.Half

def inner(u, i, domain, space=Legendre):
    r"""Compute the inner product 

    Parameters
    ----------
    u : Sympy function
    i : int
        The basis number
    domain : 2-tuple
        The true spatial domain
    space : Class instance, optional
        Either Chebyshev or Lagrange 
    
    Return
    
    .. math::
    
        (u, \psi_i)_{\omega}
    """
    A, B = -1, 1
    a, b = domain
    us = u.subs(x, a + (b-a)*(x-A)/(B-A)) 
    if space == Legendre:
        v = Legendre.basis(i)
        uv = lambda xj: sp.lambdify(x, us)(xj)*v(xj)
        return quad(uv, A, B)[0]
    elif space == Chebyshev:
        us = us.subs(x, sp.cos(x))
        uv = sp.lambdify(x, us)
        A, B = 0, np.pi
        return quad(uv, A, B, weight='cos', wvar=i)[0]
        # Alternative implementation. See https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.quad.html
        #v = Chebyshev.basis(i)
        #uv = lambda xj: sp.lambdify(x, us)(xj)*v(xj)
        #return quad(uv, A, B, weight='alg', wvar=(-0.5, -0.5))[0]

The solution for either Legendre or Chebyshev is now to compute

\[ \hat{u}_i = \frac{(u, \psi_i)_{\omega}}{\|\psi_i\|_{\omega}^2}, \quad i=0,1,\ldots, N, \]

where \(\psi_i(x)\) is either the i’th Legendre or Chebyshev polynomial, whereas the weight \(\omega\) will be either 1 or \((1-x^2)^{-1/2}\), respectively.

A lambda function to compute the coefficients of any function \(u(x), x \in [a, b]\) for either Legendre or Chebyshev polynomials is:

uhat = lambda u, j, domain, space: inner(u, j, domain, space) / sq_L2_norm(j, space)

For the collocation method we will may simply reuse code from lagrange.py, and evaluate using Chebyshev points \(x_j = \cos (j \pi / N), j=0, \ldots, N\). However, since this implementation is not optimal in terms of roundoff errors (and it is not very efficient), we will instead make use of the BarycentricInterpolator from Scipy.

We also need a function that computes the \(L^2\) error norm for the different methods:

def L2_error(N, ue, domain=(-1, 1)):
    a, b = domain
    A, B = -1, 1
    xj = np.linspace(domain[0], domain[1], 200)
    ues = sp.lambdify(x, ue)
    uej = ues(xj)
    u0 = [uhat(ue, j, domain, Legendre) for j in range(N)]
    u1 = [uhat(ue, j, domain, Chebyshev) for j in range(N)]
    err = np.zeros((3, N+1))
    for n in range(1, N+1):
        uj = Legendre(u0[:(n+1)], domain=domain)(xj).astype(float)
        err[0, n] = np.sqrt(np.trapz((uj-uej)**2, dx=xj[1]-xj[0]))
        uj = Chebyshev(u1[:(n+1)], domain=domain)(xj).astype(float)
        err[1, n] = np.sqrt(np.trapz((uj-uej)**2, dx=xj[1]-xj[0]))
        xi = np.cos(np.arange(n+1)*np.pi/n)
        xX = a + (b-a)/(B-A)*(xi-A)
        #ll = Lagrangebasis(xX)
        #ul = Lagrangefunction(ues(xX), ll)
        #err[2, n] = np.sqrt(np.trapz((sp.lambdify(x, ul)(xj)-uej)**2, dx=xj[1]-xj[0])) 
        ll = BarycentricInterpolator(xX, ues(xX))
        err[2, n] = np.sqrt(np.trapz((ll(xj)-uej)**2, dx=xj[1]-xj[0]))  
    return err

Note that the collocation method needs to be recomputed altogether for each new n because the interpolation points changes, whereas Chebyshev/Legendre methods simply compute one coefficient for a given n. Note that it would be possible to use collocation with a mapping to the reference domain instead in order to save time.

1.2. Solve for any of the given functions

We are now ready to attack any of the 5 listed functions in the weekly assignments. Any of the 5 functions can now be solved and the L2-error plotted using the below function main.

def main(N, u, domain=(-1, 1)):
    error = L2_error(N, u, domain)
    plt.loglog(abs(np.array(error.T, dtype=float)))
    plt.legend(['Legendre', 'Chebyshev', 'Collocation'])

For example, for

1. \(u(x) = |x|, \quad x \in [-1, 1]\)

This is a discontinuous solution and as such global spectral methods will struggle to capture it well.

main(20, abs(x))

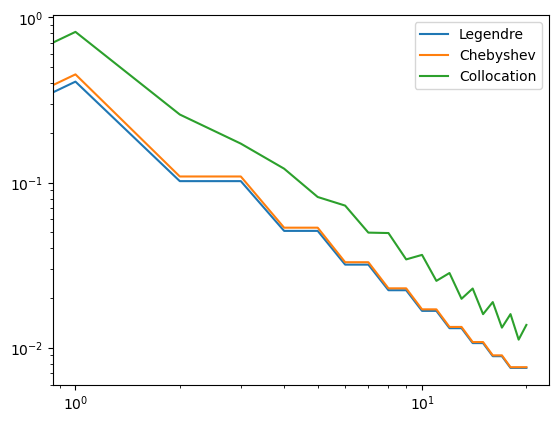
The convergence is slow due to the discontinuity. The zigzag pattern is due to the function \(u(x)=|x|\) being even, such that all odd coefficients (Chebyshev/Legendre) are zero. Hence we get is the same error using \(2n\) or \(2n+1\) basis functions for Legendre/Chebyshev.

For all functions you should find that Legendre and Chebyshev are slightly better than collocation at low N. However, the roundoff error is very good for the collocation. The roundoff error is observed when the error cannot decrease any further. The good roundoff is mainly due to the BarycentricInterpolator class, which is implemented very well. You can read more about barycentric interpolation in the very nice paper by Berrut and Trefethen. Note that the Chebyshev method would have better roundoff if we implemented a fast transform to the real space before computing the L2-error.