Solving PDEs with the method of weighted residuals

MATMEK-4270

Prof. Mikael Mortensen, University of Oslo

Recap

We have until now considered the approximation of a function \(u(x)\) using a function space \(V_N = \text{span}\{\psi_j\}_{j=0}^N\)

\[ u_N(x) \approx u(x), \quad u_N(x) = \sum_{j=0}^N \hat{u}_j \psi_j(x) \]

In order to find the unknowns (degrees of freedom) \(\{\hat{u}_j\}_{j=0}^N\) we have considered the error \(e=u_N-u\) through various methods

  • Variational methods
    • Galerkin
    • Least squares
  • Collocation
    • Lagrange polynomials

We will now learn to approximate \(\small u(x)\) by \(\small u_N(x)\) such that it satisfies a linear equation

\[ \mathcal{L}(u) = f \]

where the generic operator \(\mathcal{L}(u)\) can represent anything, like

\[ \begin{align*} u &= f \\ u' &= f \\ u'' &= f \\ u'' +\alpha u' + \lambda u &= f \\ \frac{d}{dx}\left(\alpha \frac{d u}{dx}\right) &= f \end{align*} \]

Note

Function approximation is then simply the case \(u=f\), such that \(u_N \approx f\).

Define a new error measure (the residual) that we ultimately want to be zero

\[ \mathcal{R} = \mathcal{L}(u)-f \]

and create a “numerical” residual by inserting for \(u = u_N\)

\[ \mathcal{R}_N = \mathcal{L}(u_N)-f \]

The task now is to minmize \(\mathcal{R}_N\) in order to find the unknowns that are still \(\{\hat{u}_j\}_{j=0}^N\).

Note

For function approximation \(\mathcal{R}_N = e = u_N - f = u_N - u\).

The method of weighted residuals (MWR)

is defined such that the residual (with \(u_N \in V_N\)) must satisfy

\[ (\mathcal{R}_N, v) = 0 \quad \forall \, v \in W \]

for some (possibly different) functionspace \(W\).

This is a generic method, where the choice of \(V_N\) and \(W\) fully determines the method.

Note the similarity to function approximation

\[ (u_N - u, v) = (e, v) = 0 \]

Now we have instead the slightly more complicated

\[ (\mathcal{L}(u_N)-f, v) = (\mathcal{R}_N, v) = 0 \]

The Galerkin method is a MWR with \(W=V_N\)

Find \(u_N \in V_N\) such that

\[ (\mathcal{R}_N, v)=(\mathcal{L}(u_N)-f, v)=0, \quad \forall \, v \in V_N \]

The residual (or error) is orthogonal to all the test functions. We can also write this as

\[ (\mathcal{L}(u_N)-f, \psi_j)=0, \quad j=0,1,\ldots, N \]

The least squares method is a MWR with \(\small W=\text{span}\{\frac{\partial \mathcal{R}_N}{\partial \hat{u}_j}\}_{j=0}^N\)

since \[ \frac{\partial (\mathcal{R_N}, \mathcal{R}_N)}{\partial \hat{u}_j} = 0, \quad j = 0, 1, \ldots, N \]

can be written as

\[ \left(\mathcal{R}_N, \frac{\partial \mathcal{R}_N}{\partial \hat{u}_j}\right)=0, \quad j = 0, 1, \ldots, N \]

The collocation method is to find

\[ \mathcal{R}_N(x_j) = 0, \quad j = 0, 1, \ldots, N \]

for some chosen mesh points \(\{x_j\}_{j=0}^N\).

If we write the inner products \((\mathcal{R}_N, v)\) as

\[ (\mathcal{R}_N, \psi_j) = 0, \quad j=0, 1, \ldots, N \]

and use Dirac’s delta function as test functions \(\psi_j = \delta(x-x_j)\), then

\[ (\mathcal{R}_N, \psi_j) = \int_{\Omega} \mathcal{R}_N(x) \delta(x-x_j) dx = \mathcal{R}_N(x_j) \]

So the collocation method can technically also be considered a MWR!

However, collocation is not a regular variational method since \(\delta(x)\) is a distribution and

\[W \ne \text{span}\{\delta(x-x_i)\}_{i=0}^N\]

The MWR is thus

Find \(u_N \in V_N\) such that

\[ (\mathcal{R}_N, v) = 0, \quad \forall v \in W \]

\(N+1\) equations for \(N+1\) unknowns!

Find \(\{\hat{u}_j\}_{j=0}^N\) by choosing \(N+1\) test functions for \(W\). Choose test functions (basis functions for \(W\)) using either one of:

  • Galerkin
  • Least squares
  • Collocation

First example - Poisson’s equation

\[ \begin{align} u''(x) &= f(x), \quad x \in (-1, 1) \\ u(-1) &= u(1) = 0 \end{align} \]

Find \(u_N \in V_N\) such that

\[ (u_N''-f, v) = 0, \quad \forall \, v \in W \]

How to choose \(V_N\) and \(W\)? How do we satisfy the 2 boundary conditions?

If we choose all the trial functions \(\psi_j\) such that

\[ \psi_j(\pm 1) = 0 \]

then, regardless the values of \(\{\hat{u}_j\}_{j=0}^N\)

\[ u_N(\pm 1) = \sum_{j=0}^N \hat{u}_j \psi_j(\pm 1) = 0 \]

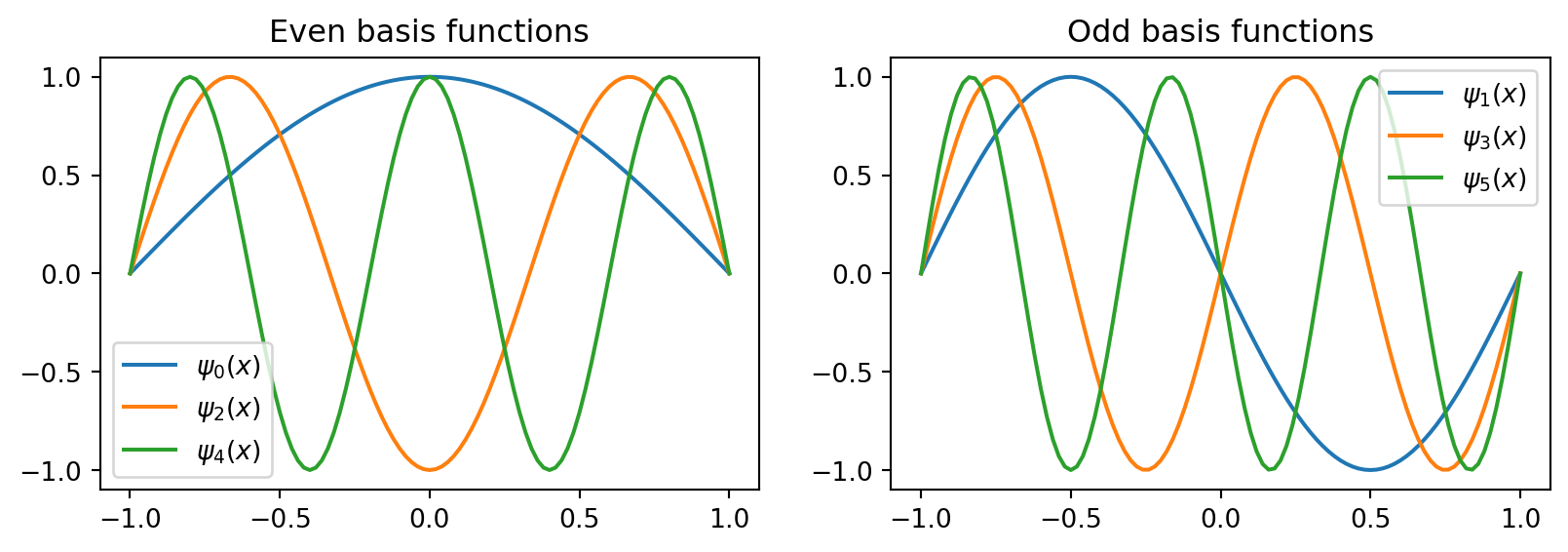
First choice for trial functions in \(V_N\)

The domain is \([-1, 1]\), so a sensible choice for \(j\ge 0\) is

\[ \psi_j(x) = \sin(\pi (j+1) (x+1)/2) \]

The \((j+1)\) is there because we start at \(j=0\) and \(\sin(0)=0\) is not a basis function. These sines are also alternating odd/even functions.

In comparison the (unmapped) sine functions \(\sin(\pi(j+1)x), x \in [-1, 1]\) are odd for all integer \(j \ge 0\)

Solve Poisson’s equation

Insert for \(u_N=\sum_{j=0}^N \hat{u}_j \psi_j\) and \(v=\psi_i\) and obtain the linear algebra problem

\[ \sum_{j=0}^N \left(\psi''_j, \psi_i \right) \hat{u}_j = (f, \psi_i), \quad i = 0, 1, \ldots, N \]

Consider using integration by parts

\[ \int_{a}^b u' v dx = -\int_a^b u v' dx + [u v]_{a}^b \]

Set \(u=u'\) to obtain

\[ \int_{a}^b u'' v dx = -\int_a^b u' v' dx + [u' v]_{a}^b \]

\[ \longrightarrow \left(\psi''_j, \psi_i \right) = -\left( \psi'_j, \psi'_i \right) + [\psi'_j \psi_i]_{-1}^1 \]

Poisson’s equation with integration by parts

Since \(\psi_j(\pm 1) = 0\) for all \(j\ge 0\) we get that

\[ \left(\psi''_j, \psi_i \right) = -\left( \psi'_j, \psi'_i \right) + \cancel{[\psi'_j \psi_i]_{-1}^1} \]

Hence Poisson’s equation gets two alternative forms

\[ \sum_{j=0}^N \left(\psi''_j, \psi_i \right) \hat{u}_j = (f, \psi_i), \quad i = 0, 1, \ldots, N \tag{1} \]

\[ \sum_{j=0}^N \left(\psi'_j, \psi'_i \right) \hat{u}_j = -(f, \psi_i), \quad i = 0, 1, \ldots, N \tag{2} \]

Note

The integration by parts is not really necessary here, as it is actually just as easy to compute \(\left(\psi''_j, \psi_i \right)\) as \(\left(\psi'_j, \psi'_i \right)\)!

Find the stiffness matrix \((\psi''_j, \psi_i)\)

\[ \begin{align*} (\psi''_j, \psi_i) &= \Big((\sin( \pi (j+1) (x+1)/2))'', \, \sin(\pi (i+1)(x+1)/2) \Big) \\ &= -\frac{(j+1)^2\pi^2}{4} \Big(\sin(\pi (j+1)(x+1)/2), \, \sin(\pi (i+1) (x+1)/2) \Big) \\ &= -\frac{(j+1)^2 \pi^2}{4} \delta_{ij} \end{align*} \]

Solve problem

\[ \sum_{j=0}^N \left(\psi''_j, \psi_i \right) \hat{u}_j = (f, \psi_i), \quad i = 0, 1, \ldots, N \]

\[ \longrightarrow \hat{u}_i = \frac{-4}{(i+1)^2 \pi^2}\Big(f,\, \sin( \pi (i+1)(x+1)/2)\Big), \quad i = 0, 1, \ldots, N \]

Implementation using the method of manufactured solution

from scipy.integrate import quad
x = sp.Symbol('x')
ue = (1-x**2)*sp.exp(sp.cos(sp.pi*(x-0.5)))
f = ue.diff(x, 2) # manufactured f=u''
uhat = lambda j: -(4/(j+1)**2/np.pi**2)*quad(sp.lambdify(x, f*sp.sin((j+1)*sp.pi*(x+1)/2)), -1, 1)[0]
uh = [uhat(k) for k in range(200)]
xj = np.linspace(-1, 1, 201)
sines = np.sin(np.pi/2*(np.arange(len(uh))[None, :]+1)*(xj[:, None]+1))
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 3))
uej = sp.lambdify(x, ue)(xj)
ax1.plot(xj, uej, 'b', xj, sines[:, :1] @ np.array(uh)[:1], 'k:',
         xj, sines @ np.array(uh), 'r--')
ax2.loglog(abs(np.array(uh)))
ax1.legend(['Exact', 'One coefficient', f'{200} coefficients'])
ax1.set_title('Solution');ax2.set_title(r'$|\hat{u}|$');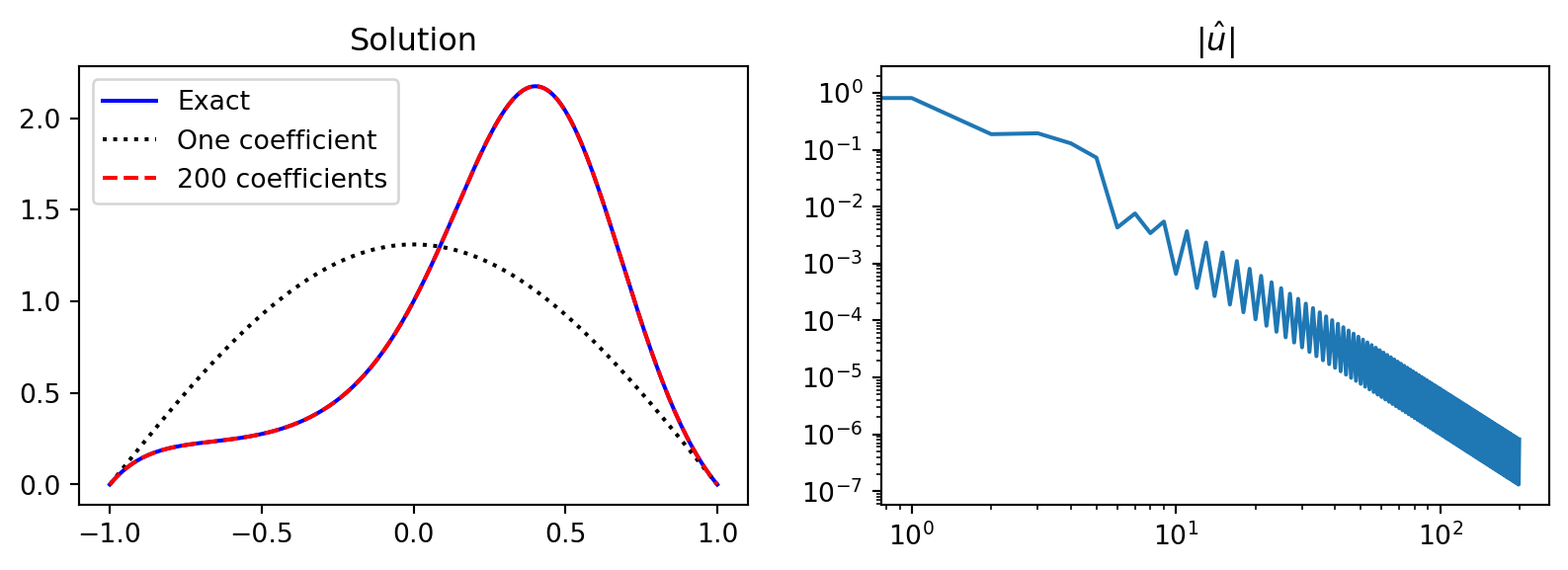

Another alternating odd/even basis can be created from Legendre polynomials \(P_j(x)\)

\[ \begin{align} \psi_j(x) &= P_j(x) - P_{j+2}(x)\\ \psi_j(\pm 1) &= 0 \end{align} \]

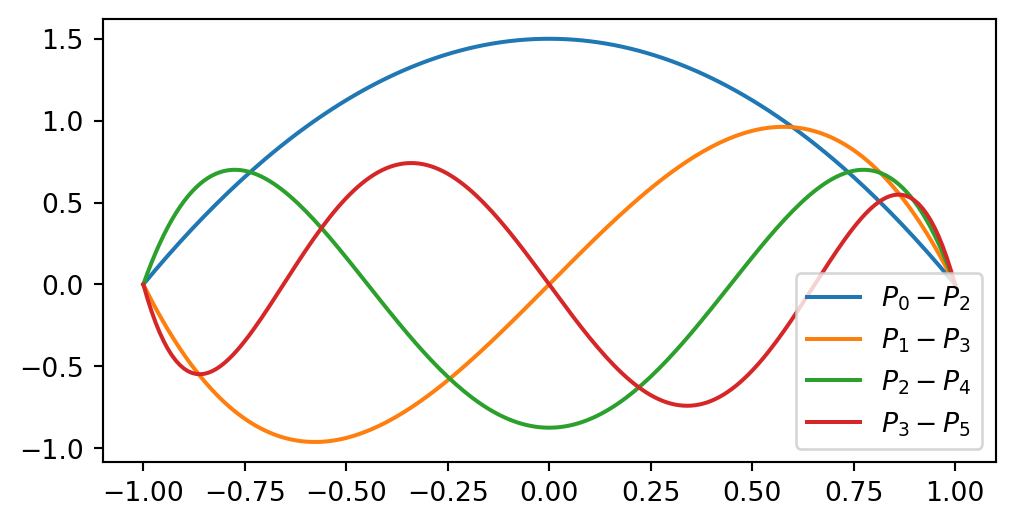
Remember that

\[ P_j(-1) = (-1)^j \quad \text{and} \quad P_j(1) = 1. \]

Hence for any \(j\) all basis functions are zero

\[ \begin{align} P_j(-1) - P_{j+2}(-1) &= (-1)^j - (-1)^{j+2} = 0 \\ P_j(1)-P_{j+2}(1) & =1-1=0 \end{align} \]

Solve Poisson’s equation with composite Legendre basis

The Legendre polynomials come with a lot of formulas, where two are \[ (P_j, P_i) = \frac{2}{2i+1}\delta_{ij} \quad \text{and} \quad (2i+3)P_{i+1} = P'_{i+2}-P'_{i} \]

The second is very useful for computing the diagonal (!) stiffness matrix

\[ \begin{align} (\psi'_j, \psi'_i) &= (P'_j-P'_{j+2}, P'_i-P'_{i+2}) \\ &= (-(2j+3) P_{j+1}, -(2i+3)P_{i+1}) \\ &= (2i+3)^2 (P_{j+1}, P_{i+1}) \\ &= (2i+3)^2 \frac{2}{2(i+1)+1} \delta_{i+1,j+1} \\ &= (4i+6)\delta_{ij} \end{align} \]

\[ \text{Solve Poisson's equation: } \longrightarrow \hat{u}_i = \frac{-\left(f, \psi_i\right)}{4i+6} \]

Implementation

from numpy.polynomial import Legendre as Leg
psi = lambda j: Leg.basis(j)-Leg.basis(j+2)
fl = sp.lambdify(x, f)
def uv(xj, j): return psi(j)(xj) * fl(xj)
uhat = lambda j: (-1/(4*j+6))*quad(uv, -1, 1, args=(j,))[0]
N = 60
uL = [uhat(j) for j in range(N)]
j = sp.Symbol('j', integer=True, positive=True)
V = np.polynomial.legendre.legvander(xj, N+1)
Ps = V[:, :-2] - V[:, 2:]
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 3))
ax1.plot(xj, uej, 'b',
         xj, Ps[:, :1] @ np.array(uL)[:1], 'k:',
         xj, Ps @ np.array(uL), 'r--')
ax2.loglog(abs(np.array(uL)), '*')
ax1.legend(['Exact', 'One coefficient', f'{N} coefficients'])
ax1.set_title('Solution')
ax2.set_title(r'$|\hat{u}|$');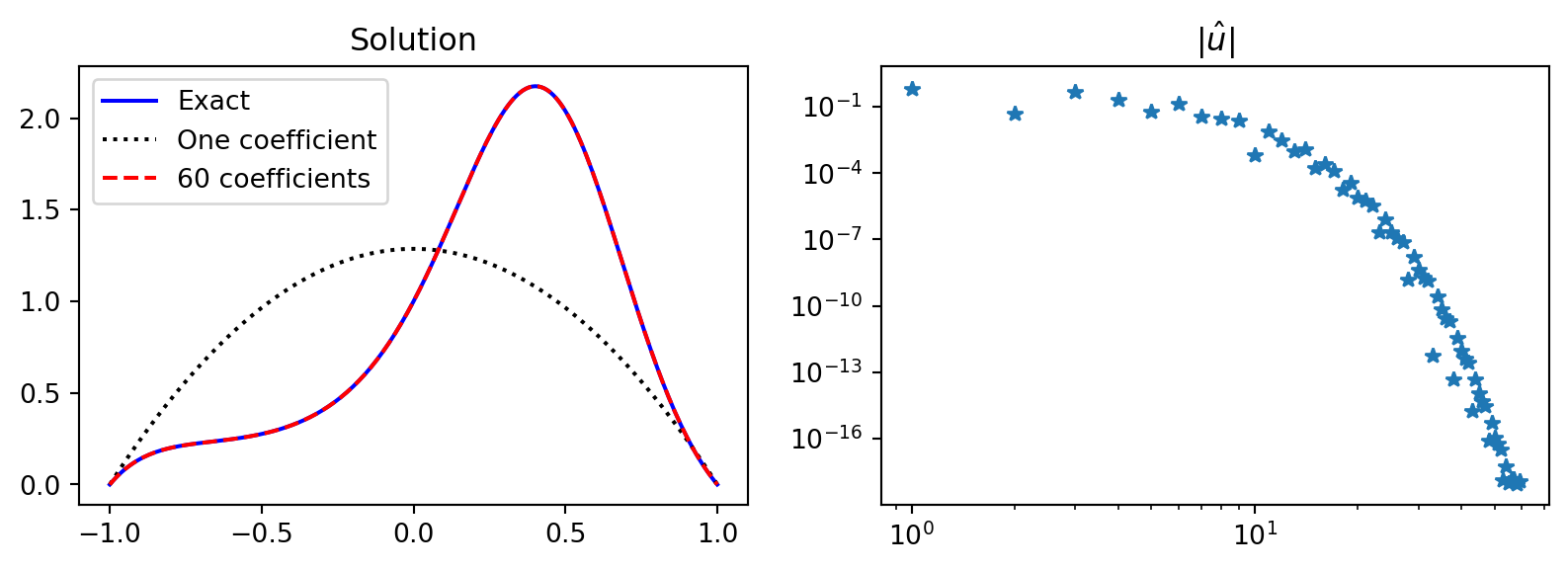

\(L^2(\Omega)\) error for sines and Legendre

\[ L^2(\Omega) = \sqrt{\int_{-1}^1(u-u_e)^2dx} \]

uh = np.array(uh)
uL = np.array(uL)
error = np.zeros((2, N))
for n in range(N):
    us = sines[:, :n] @ uh[:n]
    ul = Ps[:, :n] @ uL[:n]
    error[0, n] = np.trapz((us-uej)**2, dx=(xj[1]-xj[0]))
    error[1, n] = np.trapz((ul-uej)**2, dx=(xj[1]-xj[0]))
plt.figure(figsize=(6, 2.5))
plt.loglog(error.T)
plt.legend(['Sines', 'Legendre'])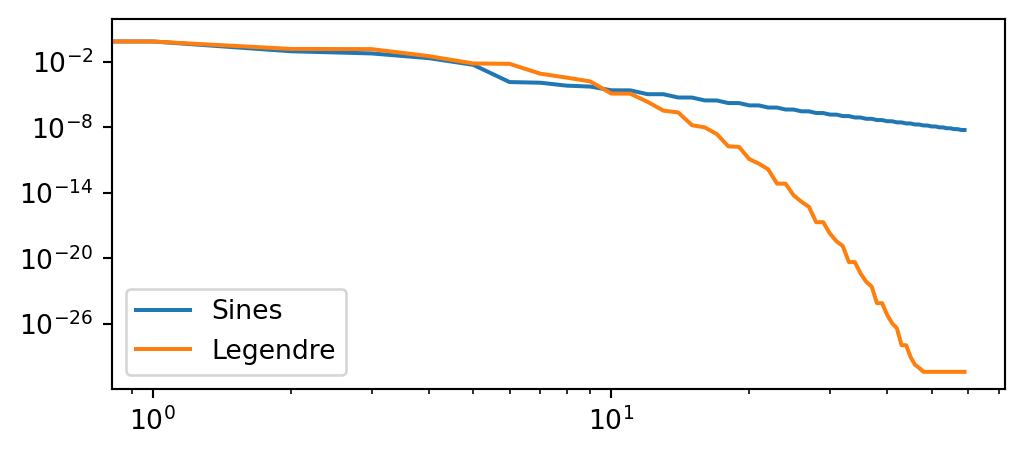

Why are the Legendre basis functions better than the sines?

All the sine basis functions \(\psi_j=\sin(\pi(j+1)(x+1)/2)\) have even derivatives equal to zero at the boundaries, unlike the chosen manufactured solution…

\[ \frac{d^{2n} \psi_j}{dx^{2n}}(\pm 1) = 0 \rightarrow \frac{d^{2n}u_N}{dx^{2n}}(\pm 1)=0, \quad n=0, 1, \ldots \]

Implementation using Shenfun

from shenfun import FunctionSpace, TestFunction, TrialFunction, inner, Dx

N = 60
VN = FunctionSpace(N+3, 'L', bc=(0, 0)) # Chooses {P_j-P_{j+2}} basis
u = TrialFunction(VN)
v = TestFunction(VN)
S = inner(Dx(u, 0, 1), Dx(v, 0, 1))
b = inner(-f, v)
uh = S.solve(b.copy())
fig = plt.figure(figsize=(6, 3))
plt.loglog(np.arange(0, N+1, 2), abs(uh[:-2:2]), '*');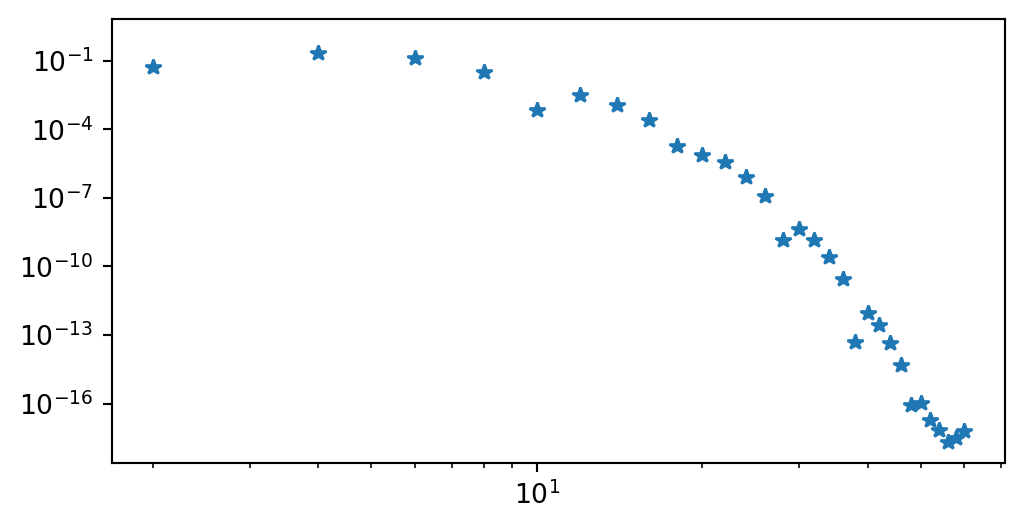

Inhomogeneous Poisson

\[ \begin{align} u''(x) &= f(x), \quad x \in (-1, 1) \\ u(-1) &= a, u(1) = b \end{align} \]

How to handle the inhomogeneous boundary conditions?

Use homogeneous \(\tilde{u}_N \in V_N\) and a boundary function \(B(x)\)

\[ u_N(x) = B(x) + \tilde{u}_N(x) \]

where \(B(-1) = a\) and \(B(1) = b\) such that

\[ u_N(-1)=B(-1)=a \quad \text{and} \quad u_N(1) = B(1) = b \]

A function that satisfies this in the current domain is

\[ B(x) = \frac{b}{2}(1+x) + \frac{a}{2}(1-x) \]

Solve Poisson

Insert for \(u_N\) into \((R_N, v) = 0\):

\[ \Big( (B(x)+\tilde{u}_N)'' - f, v \Big) = 0 \]

Since \(B(x)\) is linear \(B''=0\) and we get the homogeneous problem

\[ \Big( \tilde{u}^{''}_N - f, v \Big) = 0 \]

Solve exactly as before for \(\tilde{u}_N\) and the solution will be in the end

\[ u_N(x) = B(x) + \tilde{u}_N \]

Implementation

ue = sp.exp(sp.cos(x-0.5))
f = ue.diff(x, 2)
fl = sp.lambdify(x, f)
def uv(xj, j): return psi(j)(xj) * fl(xj)
uhat = lambda j: (-1/(4*j+6))*quad(uv, -1, 1, args=(j,))[0]
N = 30
utilde = [uhat(k) for k in range(N)]
a, b = ue.subs(x, -1), ue.subs(x, 1)
B = b*(1+x)/2 + a*(1-x)/2
M = 50
xj = np.linspace(-1, 1, M+1)
V = np.polynomial.legendre.legvander(xj, N+1)
Ps = V[:, :-2] - V[:, 2:]
Bs = sp.lambdify(x, B)(xj)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(9, 6))
ax1.plot(xj, sp.lambdify(x, ue)(xj), 'b',
         xj, Ps[:, :1] @ np.array(utilde)[:1] + Bs, 'k:',
         xj, Ps @ np.array(utilde) + Bs, 'r--')
ax2.loglog(abs(np.array(utilde)), '*')
ax1.legend(['Exact', 'One coefficient', f'{N} coefficients'])
ax1.set_title('Solution')
ax2.set_title(r'$|\hat{u}|$');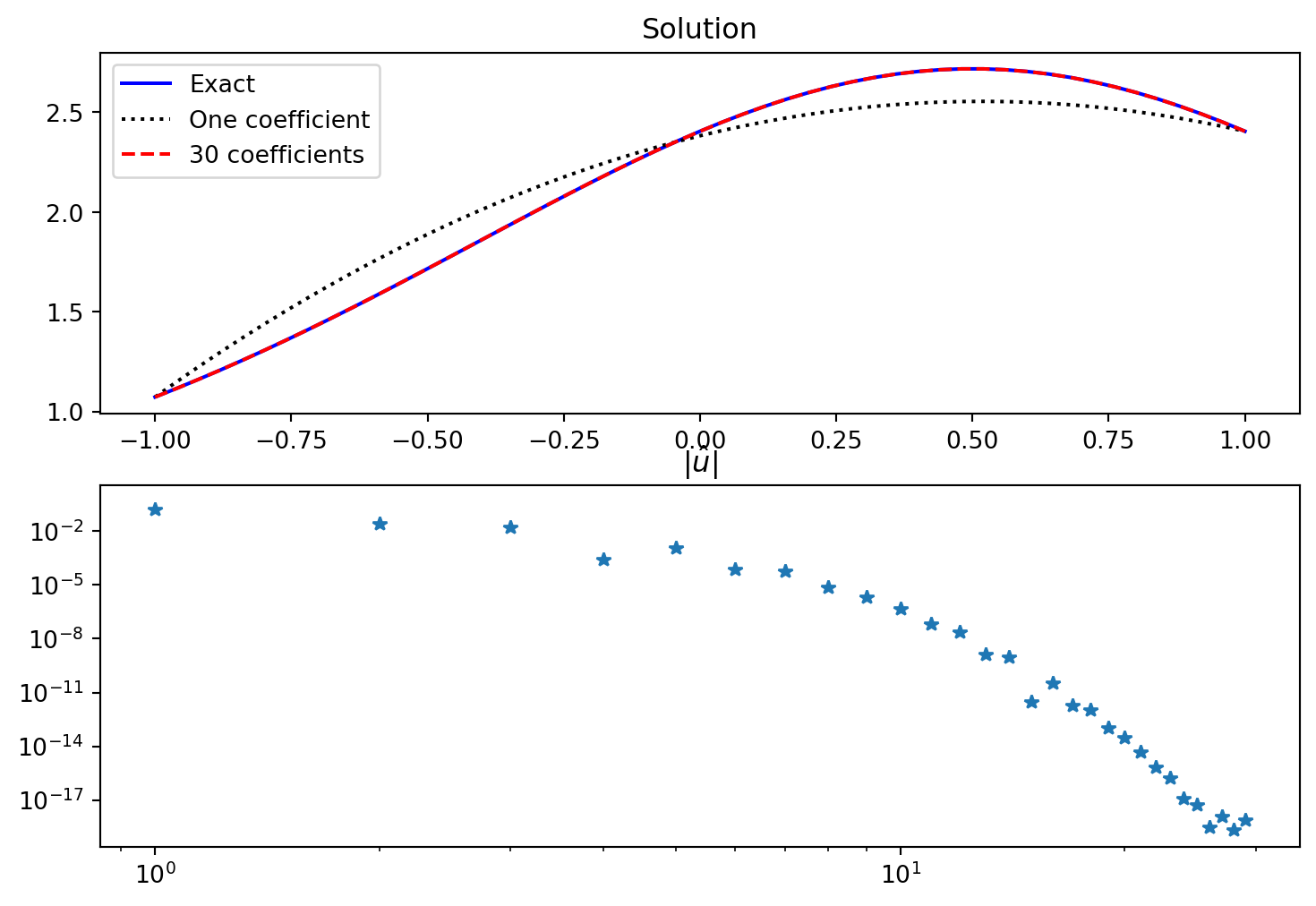

Neumann boundary conditions

\[ \begin{align} u''(x) &= f(x), \quad x \in (-1, 1) \\ u'(\pm 1) &= 0 \end{align} \]

This problem is ill-defined because if \(u\) is a solution, then \(u + c\), where \(c\) is a constant, is also a solution!

If \(u(x)\) satisfies the above problem, then

\[ (u+c)'' = u'' + \cancel{c''} = f\quad \text{and} \quad (u+c)'(\pm 1) = u'(\pm 1) = 0 \]

We need an additional constraint! One possibility is then to require

\[ (u, 1) = \int_{\Omega} u(x) dx = c \]

A well-defined Neumann problem

\[ \begin{align} u''(x) &= f(x), \quad x \in (-1, 1) \\ u'(\pm 1) &= 0 \\ (u, 1) &= c \end{align} \]

How about basis functions?

If we choose basis functions \(\psi_j\) that satisfy

\[ \psi'_j(\pm 1) = 0, \quad j=0, 1, \ldots \]

then

\[ u'_N(\pm 1) = \sum_{j=0}^N \hat{u}_j \psi'_j(\pm 1) = 0 \]

Neumann basis functions

Simplest possibility

\[ \psi_j = \cos(\pi j (x+1) / 2) \]

Easy to see that \(\psi'_j(x) = -j/2\sin(j(x+1)/2)\) and thus \(\psi'_j(\pm 1) = 0\). However, we also get that all odd derivatives are zero

\[ \frac{d^{2n+1} \psi_j}{dx^{2n+1}}(\pm 1) = 0, \quad n=0, 1, \ldots \]

Lets try to find a basis function using Legendre polynomials instead

\[ \psi_j = P_j + b(j) P_{j+1} + a(j) P_{j+2} \]

and try to find \(a(j)\) and \(b(j)\) such that \(\psi'_j(\pm 1) = 0\).

Composite Legendre Neumann basis

\[ \psi_j = P_j + b(j)P_{j+1} + a(j) P_{j+2} \]

\(\text{Using boundary conditions:} \quad P'_j(-1) = \frac{j(j+1)}{2}(-1)^j \quad \text{and} \quad P'_j(1) = \frac{j(j+1)}{2}\)

We have two conditions and two unknowns

\[\small \begin{align} \psi'_j(-1) &= P'_j(-1) + b(j)P'_{j+1}(-1) + a(j) P'_{j+2}(-1) \\ &= \left(\frac{j(j+1)}{2}-b(j)\frac{(j+1)(j+2)}{2} +a(j)\frac{(j+2)(j+3)}{2}\right)(-1)^j = 0 \end{align} \]

\[ \small \psi'_j(1) = \left(\frac{j(j+1)}{2} + b(j) \frac{(j+1)(j+2)}{2}+a(j)\frac{(j+2)(j+3)}{2}\right) = 0 \]

Solve the two equations to find \(a(j), b(j)\) and thus the Neumann basis function \(\psi_j\):

\[ b(j)=0, \, a(j) = - \frac{j(j+1)}{(j+2)(j+3)} \longrightarrow \boxed{\psi_j = P_j - \frac{j(j+1)}{(j+2)(j+3)} P_{j+2}} \]

Solve Neumann problem

Use the functionspace

\[ V_N = \text{span}\Big \{P_j - \frac{j(j+1)}{(j+2)(j+3)} P_{j+2} \Big \}_{j=0}^N \]

and try to find \(u_N \in V_N\).

However, we remember also the constraint and that

\[ (u, 1) = c \rightarrow (u_N, P_0)= c \]

since \(\psi_0 = P_0 = 1\). Insert for \(u_N\) and use orthogonality of Legendre polynomials to get

\[ \Big(\sum_{j=0}^N \hat{u}_j (P_j - \frac{j(j+1)}{(j+2)(j+3)} P_{j+2}), P_0\Big) = (P_0, P_0) \hat{u}_0 = 2 \hat{u}_0 = c \]

So we already know that \(\hat{u}_0=c/2\) and only have unknowns \(\{\hat{u}_{j}\}_{j=1}^N\) left!

Solve Neumann with Galerkin

Define

\[ \tilde{V}_N = \text{span}\Big\{P_j - \frac{j(j+1)}{(j+2)(j+3)} P_{j+2}\Big\}_{j=1}^N (= V_N \backslash \{P_0\}) \]

With Galerkin: Find \(\tilde{u}_N \in \tilde{V}_N (= \sum_{j=1}^N \hat{u}_j \psi_j)\) such that

\[ (\tilde{u}^{''}_N - f, v) = 0, \quad \forall \, v \in \tilde{V}_N \]

and use in the end

\[ u_N = \hat{u}_0 + \tilde{u}_N = \sum_{j=0}^N \hat{u}_j \psi_j \]

The linear algebra problem

We need to solve

\[ \sum_{j=1}^N(\psi^{''}_j, \psi_i) \hat{u}_j = (f, \psi_i), \quad i=1,2, \ldots, N \]

The stiffness matrix for Neumann

\[ (\psi^{''}_j, \psi_i) = -(\psi^{'}_j, \psi^{'}_i) = (\psi_j, \psi^{''}_i) \]

is fortunately diagonal (derivation later) and we can easily solve for \(\{\hat{u}_i\}_{i=1}^N\)

\[ (\psi^{''}_j, \psi_i) = a(j) (4j+6) \delta_{ij} \]

\[ \longrightarrow \hat{u}_i = \frac{(f, \psi_i)}{a(i)(4i+6)}, \quad i = 1, 2, \ldots, N \]

Derivation of \((\psi^{''}_j, \psi_i)\)

There is a series expansion for the second derivative \(P^{''}_j\)

\[ P^{''}_j = \sum_{\substack{k=0 \\ k+j \text{ even}}}^{j-2}c(k, j) P_k, \, \text{where}\, c(k, j) = (k+1/2)(j(j+1)-k(k+1)) \tag{1} \]

Hence \(P^{''}_N+a(N)P^{''}_{N+2}\) is a Legendre series ending at \(a(N)c(N-2, N)P_N\). Consider

\[ \Big(P^{''}_j+a(j)P^{''}_{j+2}, \, P_i + a(i)P_{i+2} \Big) \]

Based on the orthogonality \((P_i, P_j)=\frac{2}{2j+1}\delta_{ij}\) and (1) we get that

  • If \(i>j\) then \(\small(P^{''}_j+a(j)P^{''}_{j+2}, P_i + a(i)P_{i+2})=0\) since \(\small P^{''}_{j+2}=\sum_{k=0}^j c(k,j) P_k\)

  • If \(i< j\) then \(\small (P^{''}_j+a(j)P^{''}_{j+2}, P_i + a(i)P_{j+2})=0\) due to symmetry \((\psi^{''}_j, \psi_i) = (\psi_j, \psi^{''}_i)\)

Hence \(\Big(P^{''}_j+a(j)P^{''}_{j+2}, \, P_i + a(i)P_{i+2} \Big)\) is diagonal!

Compute \((\psi^{''}_i, \psi_i)\)

Using again the expression \(P^{''}_i = \sum_{k=0}^{i-2} c(k, i) P_{k}\)

\[ \small \begin{multline} \Big(P^{''}_i+a(i)P^{''}_{i+2}, P_i+a(i)P_{i+2}\Big) = \\ \cancel{(P^{''}_i, P_i)} + \cancel{a(i)(P^{''}_i, P_{i+2})} + a(i)(P^{''}_{i+2}, P_i) + \cancel{a^2(i)(P^{''}_{i+2}, P_{i+2})} \end{multline} \]

All cancellations because of orthogonality and \(P^{''}_i = \sum_{k=0}^{i-2} (\cdots) P_{k}\)

\[ \small \begin{align} a(i)(P^{''}_{i+2}, P_i) &= a(i) \sum_{\substack{k=0 \\ k+i \text{ even}}}^{i} \Big( (k+1/2)((i+2)(i+3)-k(k+1))P_k, \, P_i \Big) \\ &= a(i)(i+1/2)((i+2)(i+3)-i(i+1)) (P_i, P_i) \\ &= a(i)(4i+6) \end{align} \]

Hence we get the stiffness matrix

\[ (\psi^{''}_j, \psi_i) = a(i) (4i+6) \delta_{ij} \]

Implementation

Use manufactured solution that we know satisfies the boundary conditions

\[ u(x) = \int (1-x^2)\cos (x-1/2)dx \]

ue = sp.integrate((1-x**2)*sp.cos(x-sp.S.Half), x)
f = ue.diff(x, 2) # manufactured f
c = sp.integrate(ue, (x, -1, 1)).n() # constraint c
psi = lambda j: Leg.basis(j)-j*(j+1)/((j+2)*(j+3))*Leg.basis(j+2)
fj = sp.lambdify(x, f)
def uv(xj, j): return psi(j)(xj) * fj(xj)
def a(j): return -j*(j+1)/((j+2)*(j+3))
uhat = lambda j: 1/(a(j)*(4*j+6))*quad(uv, -1, 1, args=(j,))[0]
N = 30; uh = np.zeros(N); uh[0] = c/2
uh[1:] = [uhat(k) for k in range(1, N)]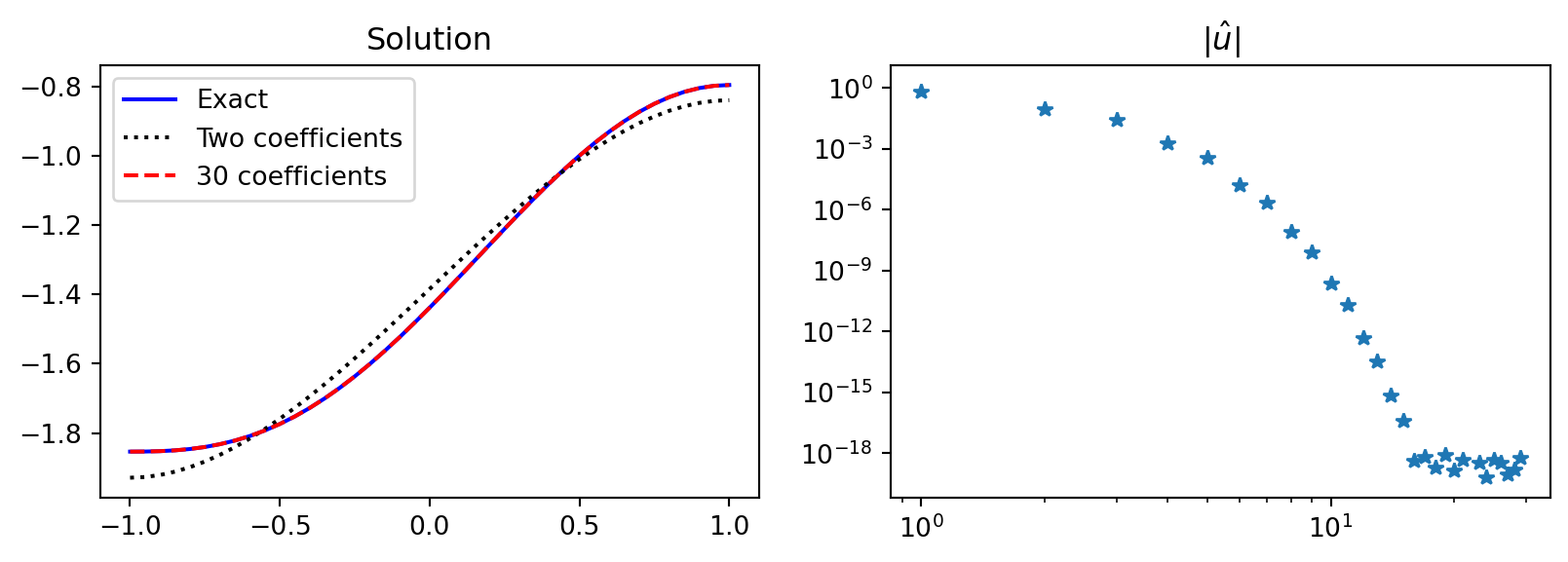

More about Neumann boundary conditions

We have used basis functions that satisfied

\[ \psi^{'}_j(\pm 1) = 0 \]

However, this was not strictly necessary! Neumann boundary conditions are often called natural conditions and we can implement them directly in the variational form:

\[ (\psi^{''}_j, \psi_i) = -(\psi^{'}_j, \psi{'}_i) + [\psi^{'}_j \psi_i]_{-1}^{1} \]

Enforce boundary conditions weakly using \(\psi^{'}_j(-1)=a, \psi^{'}_j(1)=b\):

\[ (\psi^{''}_j, \psi_i) = -(\psi^{'}_j, \psi{'}_i) + b \psi_i(1) - a \psi_i(-1) \]

Homogeneous Neumann (\(a=b=0\)):

\[ (\psi^{''}_j, \psi_i) = -(\psi^{'}_j, \psi{'}_i) \]

Implementation

Using basis function \(\psi_j(x) = P_j(x)\) that have \(\psi^{'}_j(\pm 1) \ne 0\)

psi = lambda j: Leg.basis(j)
def uf(xj, j): return psi(j)(xj) * fj(xj)
def uv(xj, i, j): return -psi(i).deriv(1)(xj) * psi(j).deriv(1)(xj)
fhat = lambda j: quad(uf, -1, 1, args=(j,))[0]
N = 20
# Compute the stiffness matrix (not diagonal)
S = np.zeros((N, N))
for i in range(1, N):
    for j in range(i, N):
        S[i, j] = quad(uv, -1, 1, args=(i, j))[0]
        S[j, i] = S[i, j]
S[0, 0] = 1 # To fix constraint uh[0] = c/2
fh = np.zeros(N); fh[0] = c/2
fh[1:] = [fhat(k) for k in range(1, N)]
fh = np.array(fh, dtype=float)
uh = np.linalg.solve(S, fh)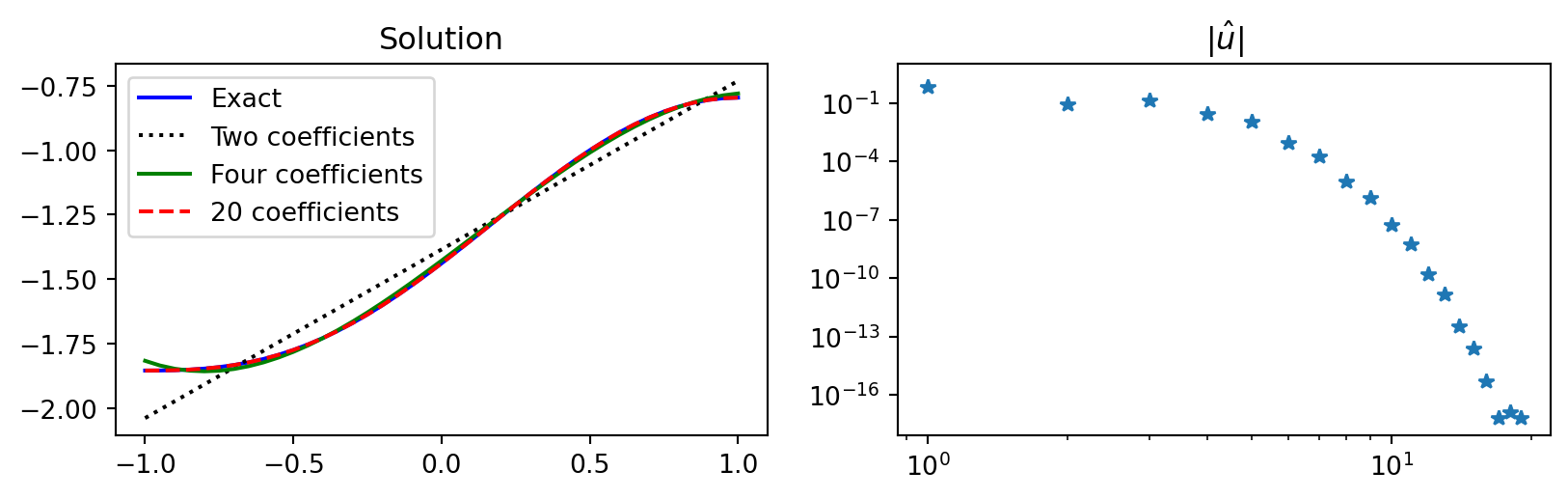

Dense stiffness matrix \((\psi'_j, \psi'_i)\)

Using basis function \(\psi_j = P_j\) leads to a dense stiffness matrix

plt.spy(S)

and thus the need for the linear algebra solve \(\boldsymbol{\hat{u}} = S^{-1} \boldsymbol{f}\)

uh = np.linalg.solve(S, fh)

Chebyshev basis functions

  • Exactly the same approach as for Legendre, only with a weighted inner product \[ (u, v)_{\omega} = \int_{-1}^1 \frac{u v}{\sqrt{1-x^2}}dx \]

  • For Dirichlet boundary conditions: Find \(u_N \in V_N = \text{span}\{T_i-T_{i+2}\}_{i=0}^N\) such that \[ (\mathcal{R}_N, v)_{\omega} = 0, \quad \forall \, v \in V_N \] The basis functions \(\psi_i=T_i-T_{i+2}\) satisfy \(\psi_i(\pm 1)=0\).

  • For Neumann boundary conditions, the basis functions are slightly different since \[ T'_k(-1) = (-1)^{k+1} k^2 \quad \text{and} \quad T'_{k}(1) = k^2 \] The basis functions \(\phi_k = T_{k} - \left(\frac{k}{k+2}\right)^2 T_{k+2}\) satisfy \(\phi'_k(\pm 1) = 0\).

  • Inhomogeneous boundary conditions are handled like for Legendre with the same boundary function \(B(x)\).

Collocation

Consider the Dirichlet problem

\[ \begin{align} u''(x) &= f(x), \quad x \in (-1, 1) \\ u(-1) = a \quad &\text{and} \quad u(1) = b \end{align} \]

To solve this problem with collocation we use a mesh \(\boldsymbol{x}=\{x_i\}_{i=0}^N\), where \(x_0=-1\) and \(x_N=1\). The solution, using Lagrange polynomials, is

\[ u_N(x) = \sum_{i=0}^N \hat{u}_i \ell_i(x) \]

We then require that the following \(N+1\) equations are satisfied

\[ \begin{align} \mathcal{R}_N(x_i) &= 0, \quad i=1, 2, \ldots, N-1 \\ u(x_0) = a \quad &\text{and} \quad u(x_N) = b \end{align} \]

where \(\mathcal{R}_N(x) = u^{''}_N(x)-f(x)\).

Solve by inserting for \(u_N\) in \(\mathcal{R}_N\)

We get the \(N-1\) equations for \(\{\hat{u}_j\}_{j=1}^{N-1}\)

\[ \sum_{j=0}^N \hat{u}_j \ell''_j(x_i) = f(x_i), \quad i = 1, 2, \ldots, N-1 \]

in addition to the boundary conditions: \(\hat{u}_0=u_N(x_0)=a\) and \(\hat{u}_N=u_N(x_N)=b\).

The matrix \(D^{(2)} = (d^{(2)}_{ij})=(\ell^{''}_j(x_i))_{i,j=0}^N\) is dense. How do we compute it?

Note

Using the Sympy Lagrange functions is numerically unstable

Another useful form of the Lagrange polynomials

\[ \ell_j(x) = \prod_{\substack{0 \le m \le N \\ m \ne j}} \frac{x-x_m}{x_j-x_m} \]

A small rearrangement leads to

\[ \ell_j(x) = \ell(x) \frac{w_j}{x-x_j}, \]

where

\[ \ell(x) = \prod^N_{\substack{i=0}}(x-x_i) \quad \text{and} \quad w_j = \frac{1}{\ell'(x_j)}= \frac{1}{\prod^N_{\substack{i=0 \\ i \neq j}} (x_j - x_i)} \]

Here \((w_j)_{j=0}^N\) are the barycentric weights. Scipy will give you these weights: from scipy.interpolate import BarycentricInterpolator

The main advantage of the Barycentric approach is numerical stability

And we can obtain the derivative matrix \(d_{ij} = \ell'_j(x_i)\) as

\[ \begin{align*} d_{ij} &= \frac{w_j}{w_i(x_i-x_j)}, \quad i \, \neq j, \\ d_{ii} &= -\sum_{\substack{j=0 \\ j \ne i}}^N d_{ij}. \end{align*} \]

from scipy.interpolate import BarycentricInterpolator
def Derivative(xj):
    w = BarycentricInterpolator(xj).wi
    W = w[None, :] / w[:, None]
    X = xj[:, None]-xj[None, :]
    np.fill_diagonal(X, 1)
    D = W / X
    np.fill_diagonal(D, 0)
    np.fill_diagonal(D, -np.sum(D, axis=1))
    return D

Numpy broadcasting!

W is the matrix with items \(w_j / w_i\). \(w_i\) varies along the first axis and is thus w[:, None]. \(w_j\) varies along the second axis and is w[None, :]. Likewise \(x_i\) is xj[:, None] and \(x_j\) is xj[None, :]

Higher order derivative matrices \(d^{n}_{ij} = \ell^{(n)}_j(x_i)\) can be computed recursively

\[ \begin{align*} d^{(n)}_{ij} &= \frac{n}{x_i-x_j}\left(\frac{w_j}{w_i} d^{(n-1)}_{ii} - d^{(n-1)}_{ij} \right) \\ d^{(n)}_{ii} &= -\sum_{\substack{j=0 \\ j \ne i}}^N d^{(n)}_{ij} \end{align*} \]

def PolyDerivative(xj, m):
    w = BarycentricInterpolator(xj).wi * (2*(len(xj)-1))
    W = w[None, :] / w[:, None]
    X = xj[:, None]-xj[None, :]
    np.fill_diagonal(X, 1)
    D = W / X
    np.fill_diagonal(D, 0)
    np.fill_diagonal(D, -np.sum(D, axis=1))
    if m == 1: return D
    D2 = np.zeros_like(D)
    for k in range(2, m+1):
        D2[:] = k / X * (W * D.diagonal()[:, None] - D)
        np.fill_diagonal(D2, 0)
        np.fill_diagonal(D2, -np.sum(D2, axis=1))
        D[:] = D2
    return D2

Use Chebyshev points for spectral accuracy

\[ x_i = \cos(i \pi / N) \]

The barycentric weights are then simply

\[ w_i = (-1)^{i} c_i, \quad c_i = \begin{cases} 0.5 \quad i=0 \text{ or } i = N \\ 1 \quad \text{ otherwise} \end{cases} \tag{1} \]

N = 8
xj = np.cos(np.arange(N+1)*np.pi/N)
w = BarycentricInterpolator(xj).wi * 2*N
w
array([ 0.5, -1. ,  1. , -1. ,  1. , -1. ,  1. , -1. ,  0.5])

Note

The weights are only relative, so we have here scaled by \(2N\) to get (1)

And then we solve any equation by replacing the ordinary derivatives with derivative matrices

\[ \begin{align} u''(x) &= f(x), \quad x \in (-1, 1) \\ u(-1) = a \quad &\text{and} \quad u(1) = b \end{align} \]

Let \(d^{(2)}_{ij} = \ell^{''}_j(x_i)\) for all \(i=1, \ldots, N-1\), ident the first and last rows of \(D^{(2)}\) and set \(f_0=a\) and \(f_N=b\). Solve

\[ \sum_{j=0}^N d^{(2)}_{ij} \hat{u}_j = f_i, \quad i=0, 1, \ldots, N \]

Matrix form using \(\boldsymbol{\hat{u}} = (\hat{u}_j)_{j=0}^N\) and \(\boldsymbol{f} = (f_j)_{j=0}^N\)

\[ D^{(2)} \boldsymbol{\hat{u}} = \boldsymbol{f} \]

\[ \boldsymbol{\hat{u}} = (D^{(2)})^{-1} \boldsymbol{f} \]

Implementation for Poisson’s equation

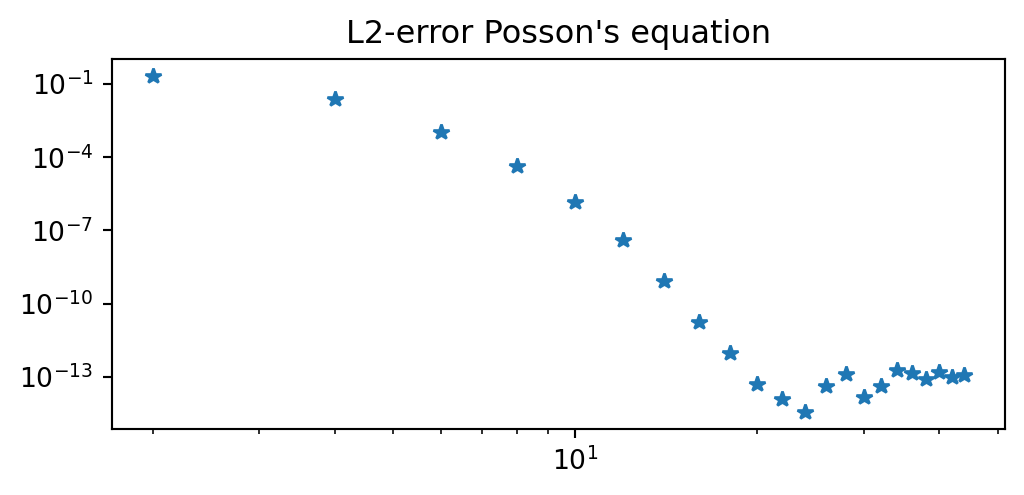
def poisson_coll(N, f, bc=(0, 0)):
    xj = np.cos(np.arange(N+1)*np.pi/N)[::-1]
    D2 = PolyDerivative(xj, 2)      # Get second derivative matrix
    D2[0, 0] = 1; D2[0, 1:] = 0      # ident first row
    D2[-1, -1] = 1; D2[-1, :-1] = 0  # ident last row
    fh = np.zeros(N+1)
    fh[1:-1] = sp.lambdify(x, f)(xj[1:-1])
    fh[0], fh[-1] = bc             # Fix boundary conditions
    uh = np.linalg.solve(D2, fh)
    return uh, D2

def l2_error(uh, ue):
    uj = sp.lambdify(x, ue)
    N = len(uh)-1
    xj = np.cos(np.arange(N+1)*np.pi/N)[::-1]
    L = BarycentricInterpolator(np.cos(np.arange(N+1)*np.pi/N)[::-1], yi=uh)
    N = 4*len(uh) # Use denser mesh to compute L2-error
    xj = np.linspace(-1, 1, N+1)
    return np.sqrt(np.trapz((uj(xj)-L(xj).astype(float))**2, dx=2./N))
ue = sp.exp(sp.cos(x-0.5))
f = ue.diff(x, 2)
bc = ue.subs(x, -1), ue.subs(x, 1)
err = []
for N in range(2, 46, 2):
    uh, D = poisson_coll(N, f, bc=bc)
    err.append(l2_error(uh, ue))
fig = plt.figure(figsize=(6, 2.5))
plt.loglog(np.arange(2, 46, 2), err, '*')
plt.title("L2-error Posson's equation");

Summary

  • Find \(u_N \in V_N\) such that \[(\mathcal{L}(u_N) - f, v) = (\mathcal{R}_N, v) = 0 \quad \forall v \in W\]

  • Differential equations are solved using the method of weighted residuals

    • Galerkin (\(W=V_N\))
    • Least squares (\(W = \text{span}\{\frac{\partial \mathcal{R}_N}{\partial \hat{u}_i}\}_{i=0}^N\))
    • Collocation (\(v = \delta(x-x_i)\))

  • Same approach as function approximation, but assembling matrices is more work!

  • Basis functions chosen to satisfy homogeneous boundary conditions (either Dirichlet or Neumann) and then a lifting function \(B(x)\) handles nonzero conditions \(u_N(x) = \sum_{i=0}^N \hat{u}_i \psi_i(x) + B(x)\)

  • Multi-dimensional problems (PDEs) can be solved using tensor-product spaces, vectorization and the Kronecker product (see lecture notes).